$$f^{'}(x)=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}$$
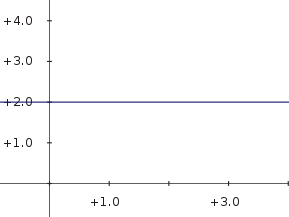
Calcularemos ahora la derivada para una función constante $f(x)=k$. En este tipo de funciones $f(x)=f(x+h)=k$. Es decir, que a medida que $x$ aumenta el valor de $f(x)$ se mantiene constante y siempre es $k$. En la función constante de nuestro gráfico $k=2$.
$$f^{'}(x)=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\dfrac{k-k}{h}=\lim_{h\to 0}\dfrac{0}{h}=0$$
Ahora ya sabemos que para cualquier función constante:
$$f(x)=k \to f^{'}(x)=0$$
Era de esperar que la derivada en una función constante nos diera cero, ya que la derivada es la variación de dicha función.
Ejemplo:
$f(x)=432 \to f^{'}(x)=0$
La derivada de cualquier tipo de constante siempre será cero.